Scottsdale Narrow Wall 2013
Given that I am at a larger company, Kleinfelder, I have even less involvement in detailed retaining wall design. However, just the other day I got an e-mail from a colleague in Las Vegas. This is a planned retaining wall in Scottsdale, Arizona, for a highway widening at a close distance to an existing retaining wall.

The question was what reduction in active pressure, if any, would result for the narrow wall (no seismic pressures involved). The colleague had already used a simple area-ratio reduction for the truncation of the passive wedge and a method by Spangler and Hardy (1982, 4th Edition, Pages 572 - 573). WASP has the capability to model a vertical limit to the rear of the active wedge, so I used it as a third method to verify their results. The planned wall varied between 13 feet high with 7 to 9 feet behind the wall to the existing wall, to 35 feet with 11 to 15 feet behind to planned wall to the existing wall.
The results generally were that the wall spacings the project required were just wide enough that there was minimal reduction in active pressure. The active pressure was reduced from simple Rankine equation (Ka = 0.31) to no less than about 0.28 for the highest wall with the closest spacing. In any case there is probably minimal benefit to the designer in reducing the pressure by less than 4 pounds per foot per foot of height (often, the geotechnical engineer's estimate of Ka is rounded to the nearest 5 pcf anyways, e.g. 35 or 40 pcf.
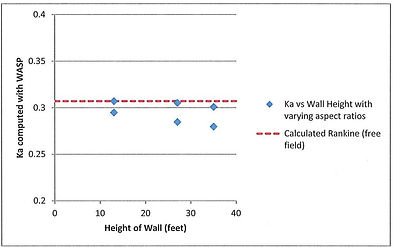
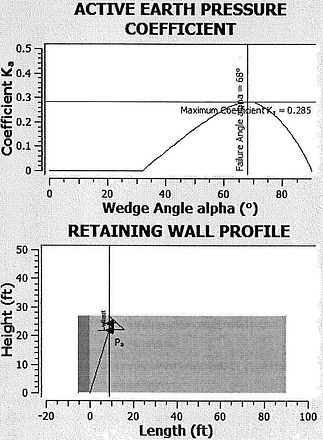
WASP assigns that the vertical portion of the slip surface adjacent to the rear wall has a complementary active pressure equal to unrevised Rankine or Coulomb Ka, which is what Spangler shows. When the walls are separated far enough, the WASP critical alpha angle does match the 45 + phi/2 degrees Rankine theory (for phi = 32 degrees in this case, the critical alpha angle is 61 degrees). As the walls get closer together, the critical angle of the base of the wedge gradually becomes steeper than 61 degrees as shown below. WASP's numerical results were nearly identical to the wedge truncation method and 10% higher than Spencer and Davis. Note that the reduction in Ka is due to the narrowing of the active wedge and the steepening of the lower slip surface, and does not require an explanation of "stress arching" to result in the lower active pressure (and WASP does not consider deformation characteristics, only free-body equilibrium).
Vista Tank Access Road Wall (Reno NV) 2008

As a geotechnical engineer, I can rarely lay claim to have fully designed a wall, segmental block walls or MSE walls being the exception. I've designed about a dozen walls. most of which have level top conditions, so WASP is not necessary (but will still come up with the same active coefficient as Mononobe-Okabe). This wall has a 5' high 2H:1V slope between the edge of road and the top of wall - the 10' distance between road and wall is required by the county (I guess if you drive off the edge of the road, they want you to start to roll before you actually go over the wall). The wall was to be constructed with import fill, so with unknown soil properties we assumed no cohesion and a friction angle of 34 degrees to represent structural fill. With this combination and 0.2 for half of the Reno peak ground acceleration, Mononobe-Okabe results in the imaginary solution. Due to the access road, the failure wedge is finite, and the wall was designable. The slope behind the far edge of the road was in clayey Tertiary volcanic soil/bedrock, so a failure surface extending further uphill was not considered. As would be expected for a Keystone wall of this height, the wall is an MSE wall reinforced with geogrid.

US 395 at Plumb Lane (Reno, Nevada) 2006

The new wall designed for PBS&J and Nevada DOT with this method is only left of the yield sign. The original wall was removed due to interchange ramp re-alignment, and was replaced with a wall oriented approximately 20 degrees further west of north. The new retaining wall is 14.3 m (46 ft) long and varies from 0 to 5.5 m (18 ft) high. The 2H:1V abutment fill above the retaining wall is retained at an oblique angle so that the average slope perpendicular to the wall is 3H:1V. The total embankment height to the level of the overlying freeway does not exceed 7.6m (25 ft). Due to the proximity of the existing slope to the bridge abutment and to prevent any risk of settlement of the abutment foundations for the overlying bridge, the replacement wall was to be built with multiple rows of tie-backs with top-down construction.
Design of the retaining wall was by AASHTO design methods (AASHTO, 17th Edition, 2002), for a peak ground acceleration of 0.39 g. Furthermore, because the proposed retaining wall was to be restrained using tie-backs, AASHTO design code required that the wall be designed for 1.5 times the peak ground acceleration, or 0.585 g. The Mononobe-Okabe method does not work for a 3H:1V slope with this horizontal seismic coefficient.
Design of the Plumb Lane retaining wall used the following parameters at the maximum wall height: Hw = 5.5m, Hsmax = 7.0m, β = 18.6 (3H:1V), ω = 0º, c = 13 kPa(250 psf), φ = 34º, δ = 17º, γ = 20 kN/m3, and Kh =
0.585g. The cohesion assigned to this wall was back-analyzed from our expectation that the wall could be excavated in 1.6-m-vertical- unsupported faces (5-ft) for shotcrete and tieback placement, which requires a short-term cohesion of at least 13 kPa. An active seismic pressure of 1.03 was determined for maximum height, and 1.08 for where the wall height was half the maximum. Including only the horizontal component of the active pressure, a horizontal active seismic pressure of 1.0 was selected for design. The failure angle for the maximum active seismic pressure varied between 17 and 24 degrees for the half-height and full-height walls, respectively, which allowed for determination of the required unbonded length of tiebacks.
While I had earlier developed draft wedge analyses for another project, this is the first project where I completed the spreadsheet and was able to verify the results fixing all significant errors. For the geotechnical report we had assigned a Kae of 1.0 based on engineering judgement and initial spreadsheet results, I completed the WASP analysis slightly afterward to justify the result, with good results, in time to include it in the bound calculations summary delivered to NDOT.
Do we know we have a cohesion of 250 psf, in what is an engineered granular sand/gravel fill? Well, despite the limitations we'd added to the special provisions, the contractor not only excavated in 5-foot lifts, they demo'ed, excavated, and left exposed the whole 18-foot-high wall at once, rather than shotcreting after each lift of tiebacks (our firm was not involved in construction monitoring!). (It is possible the unstressed tiebacks may have helped the vertical face stay up for greater than the 5-foot anchor spacing.) There was perhaps 6 inches of ravelling loss of the soil, but the face did hold vertical.
Mononobe-Okabe Spreadsheet
Excel 2010 Spreadsheet with all the bells and whistles in case you don't want to spend the time to create and proof your own.
WASP Version 1.1 with Free Demonstration Mode
Recent Blog Entries
Questions?
If you have some interest or questions about this program or the contents of this website, please feel free to contact us in the Guestbook (under "About Us") or at jpease@rtgeo.com (my day job).
